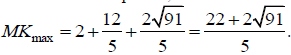Решение
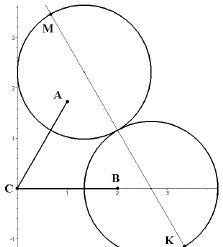
Поместим точку C в начало декартовой системы координат, а точку B на ось абсцисс, как показано на рисунке. Тогда точки C, B, A будут иметь координаты C(0,0), B(2,0), A(3/2,(3√3)/2). Геометрическое место точек K(x, y) таких, что BK : CK = 2 : 3 представляет собой окружность. Действительно,
что эквивалентно
Аналогично, геометрическое место точек M таких, что AM : MC = 1 : 2 - окружность, заданная уравнением
Чтобы расстояние между точками K (лежащей на окружности (1)) и M (на окружности (2)) было максимально, эти точки следует расположить на прямой, проходящей через центры окружностей. Таким образом, искомое максимальное расстояние равно расстоянию между центрами окружностей (1), (2) плюс длины их радиусов:
