Решение
Длина алфавита определяется количеством различных комбинаций из трех цифр, которые можно получить из панели с учетом правил и ограничений их построения. Правило шахматного коня определяет порядок перехода от одной цифры к другой (см. рисунок 3.1-1)
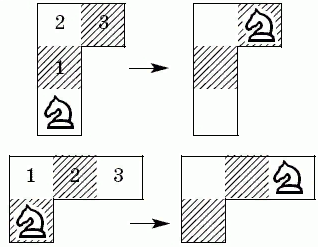
Рисунок 3.1-1 – Правило шахматного коня
Существует два варианта решения:
1. Перебор всех комбинаций вручную.
2. Автоматическое построение комбинаций с использованием графа переходов.
Способ 1.
Для поиска всех возможных комбинаций необходимо построить варианты перехода из каждой цифры клавиатуры. Возможные переходы:
1: 6, 8
2: 9,7
3: 4, 8
4: 0, 3, 9
5: пусто
6: 0, 1, 7
7: 2, 6
8: 1, 3
9: 2, 4
0: 6,4
Далее необходимо построить таблицу со всеми возможными комбинациями
Всего 46 комбинаций. В задании указано, что комбинация не может начинаться с 0 (6 комбинаций) и с 9 (5 комбинаций).
Ответ: 46–6–5 = 35 комбинаций.
Способ 2.
Необходимо задать матрицу переходов (двумерный массив), после чего осуществить перебор всех возможных трехзначных путей.
Пример задания матрицы на основе словаря на языке программирования C++ представлен в листинге 3.1-1.
Листинг 3.1-1 – Матрица переходов на основе словаря на языке программирования C++
// Словарь переходов
// ЦИФРА --> массив возможных переходов
map<int, vector<int>> table = {
{0, {4, 6}}, // переходы из 0
{1, {6, 8}}, // переходы из 1
{2, {7, 9}}, // переходы из 2
{3, {4, 8}}, // переходы из 3
{4, {3, 9, 0}}, // переходы из 4
{5, {}}, // переходы из 5
{6, {1, 7, 0}}, // переходы из 6
{7, {2, 6}}, // переходы из 7
{8,{1, 3}}, // переходы из 8
{9, {2, 4}} // переходы из 9
};
Функцию подсчета числа комбинаций можно сделать рекурсивной. На вход функции подается первая цифра и длина комбинации. Функция рекурсивно вычисляет количество таких комбинаций на основе матрицы переходов. Реализация функции на языке программирования C++ представлена в листинге 3.1-2.
Листинг 3.1-2 – Реализация функции подсчета числа комбинаций на языке программирования С++
/// Функция подсчета числа комбинаций,
/// начинающихся с цифры startNum и длиной len
/// PARAMS
/// startNum - первая цифра комбинации
/// len - длина комбинации
/// RETURN
/// количество комбинаций заданной длины,
/// начинающихся с startNum
int count(int startNum, int len)
{
// счетчик числа комбинаций
int cnt = 0;
// если последовательность нулевой длины - их 0
if (len == 0)
return 0;
// если последовательность длины 1 - их 1 (сама цифра startNum)
if (len == 1)
return 1;
else
{
// перебираем все возможные числа, в которые можно перейти
// из startNum - это указано в массиве table[startNum]
auto numbersToGo = table[startNum];
// считаем и складываем количество таких комбинаций,
// длина которых уже на 1 цифру меньше
for (int i = 0; i < numbersToGo.size(); i++)
cnt += count(numbersToGo[i], len - 1);
return cnt;
}
}
Фрагмент общей программы на языке программирования C++, запускающей в цикле подсчет числа комбинаций, представлен в листинге 3.1-3.
Листинг 3.1-3 – Фрагмент программы подсчета общего числа комбинаций на языке программирования C++
int main()
{
// счетчик комбинаций
int cnt = 0;
// перебираем все начальные цифры
for (auto it = table.begin(); it != table.end(); it++)
{
cnt += count(it->first, 3);
}
// вычитаем комбинации, начинающиеся с 0 и с 9
cnt = cnt - count(0, 3) - count(9, 3);
cout << "Total: " << cnt << endl;
}
В результате выполнения программа выдает на экран:
Total: 35
