Архив задач

Три пробирки

Имеется неограниченное количество пробирок трёх видов – А, В и С. Каждая из пробирок содержит один грамм раствора одного и того же вещества. В пробирках вида А содержится 10% раствор этого вещества, в пробирках В – 20% раствор и в С – 90% раствор. Последовательно, одну за другой, содержимое пробирок переливают в некоторую ёмкость. При этом при двух последовательных переливаниях нельзя использовать пробирки одного вида.  Какое наименьшее количество переливаний надо сделать, чтобы получить в ёмкости 20,17% раствор? Какое наибольшее количество пробирок вида C может быть при этом использовано?

  • Подсказка

    • Подсказка

    Свести решение задачи к решению уравнения в целых числах; воспользоваться свойствами делимости.
  • Решение

    • Решение

    Пусть пробирок вида А, В и С взяли соответственно a, b и с штук. По условию
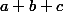
    Левая часть последнего равенства делится на 1000, следовательно на 1000 должна делиться и правая часть. Значит, наименьшее возможное значение суммы равно 1000. Покажем, что эта оценка достижима. То есть, докажем, что существуют неотрицательные целые числа a, b и с такие, что
    Последние три неравенства служат необходимым и достаточным условиям того, что удастся избежать использования пробирок одного вида при двух последовательных переливаниях. Из первых двух уравнений системы находим
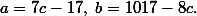
    Подставив эти выражения в последние три неравенства системы, получим

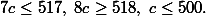
    Отсюда наибольшее значение с равно 73. После этого находим соответствующие ему значения a и b по найденным выше формулам. Они, очевидно, удовлетворяют неравенствам системы. Таким образом, разрешимость в неотрицательных целых числах системы доказана.
  • Ответ

    • Ответ

    Наименьшее количество переливаний равно 1000. При этом могут быть использованы максимум 73 пробирки вида С.