Решение
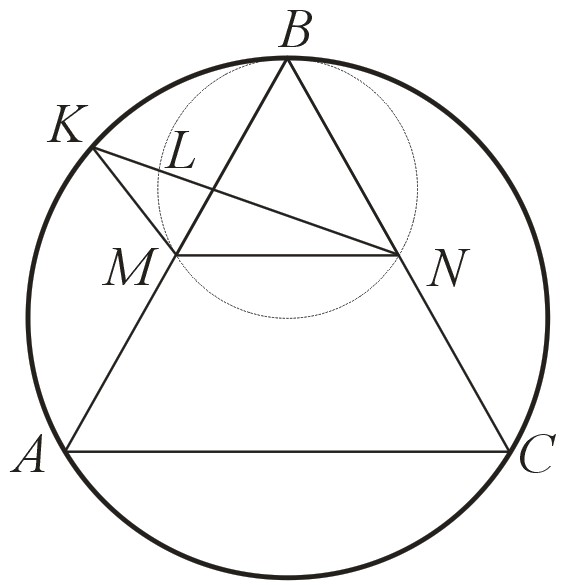
Опишем окружность вокруг треугольника BMN. Она касается внутренним образом в точке B описанной около треугольника ABC окружности, поскольку точка B и центры окружностей лежат на одной прямой. Пусть сначала точка К лежит выше горизонтальной прямой MN. Пусть L – точка пересечения отрезка KN и меньшей окружности. Угол MLN равен
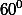
, и, следовательно, угол KLM равен
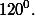
Значит, угол MKN не превосходит
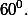
Заметим, что в приведенном рассуждении не играет никакой роли то обстоятельство, что точка К лежит на окружности. Важно лишь, что она находится выше прямой MN и вне окружности, описанной около треугольника BMN. Пусть теперь точка К расположена ниже прямой MN (этот случай на рисунке не отражен). Рассмотрим точку P, симметричную точке К относительно прямой MN. Углы MPN и MKN, очевидно, равны. Точка P лежит выше прямой MN и вне меньшей окружности. По доказанному, угол MPN не превосходит
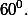
Утверждение доказано полностью.
 Опишем окружность вокруг треугольника BMN. Она касается внутренним образом в точке B описанной около треугольника ABC окружности, поскольку точка B и центры окружностей лежат на одной прямой. Пусть сначала точка К лежит выше горизонтальной прямой MN. Пусть L – точка пересечения отрезка KN и меньшей окружности. Угол MLN равен
Опишем окружность вокруг треугольника BMN. Она касается внутренним образом в точке B описанной около треугольника ABC окружности, поскольку точка B и центры окружностей лежат на одной прямой. Пусть сначала точка К лежит выше горизонтальной прямой MN. Пусть L – точка пересечения отрезка KN и меньшей окружности. Угол MLN равен