Решение
Сначала рассчитаем треугольник

.
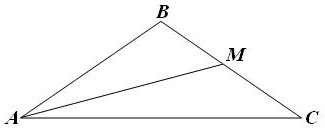
По условию углы

и

равны

, медиана

. По
теореме синусов для треугольника

откуда

.
По теореме косинусов для треугольника

откуда

. Следовательно,

.
Высота, опущенная из вершины

, равна
Площадь треугольника

:
Заметим, что радиус круга

из условия задачи больше
высоты

, но меньше боковой стороны

. Поэтому чертеж к
задаче имеет вид
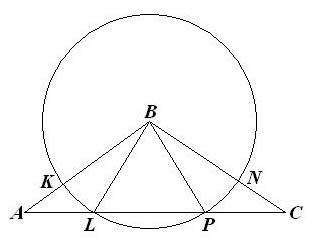
Здесь
Общая часть треугольника и круга
- это сектор

без сегмента

.
Площадь сектора равна
Найдем площадь сегмента. Для этого из треугольника

найдем угол

. Так как треугольник

равнобедренный с боковой
стороной

и высотой

, то

и

. Теперь площадь сегмента

равна
Окончательно получаем площадь общей части
Теперь можно найти отношение площадей

